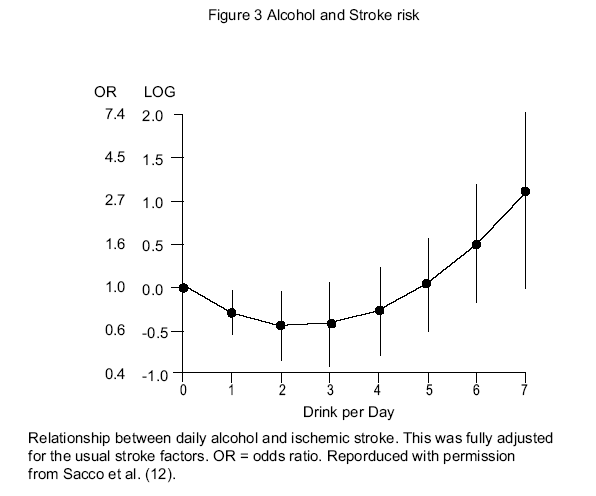
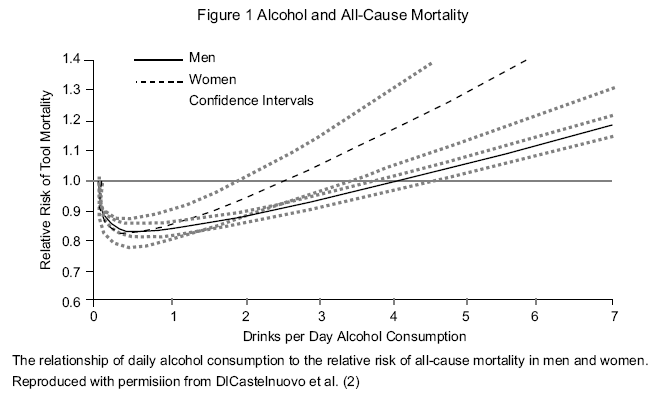
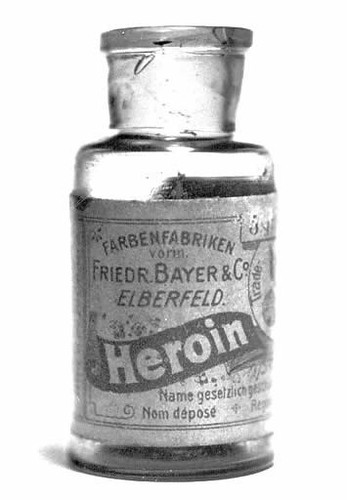
… we can say that the Great Library was an extensive collection of books associated with the famous institute of learning and research that was the shrine of the Muses in Alexandria. That much is clear. But many of the other things often claimed about it are much less clear and some of them are pure fantasy, so it’s time to turn to the list of things that the “Great Library” was not.
… we can say that the Great Library was an extensive collection of books associated with the famous institute of learning and research that was the shrine of the Muses in Alexandria. That much is clear. But many of the other things often claimed about it are much less clear and some of them are pure fantasy, so it’s time to turn to the list of things that the “Great Library” was not.
“It was the largest library in the ancient world, containing over 700,000 books.”
It is entirely possible that it was the largest library in the ancient world, though we have no way of confirming this given that we have little reliable information about the size of its collection. Despite this, popular sources regularly repeat the huge figures given for the number of books in the library in several ancient sources, and usually opt for the ones that are the highest. Shakespeare scholar Stephen Greenblatt’s popular history The Swerve: How the Renaissance Began (Vintage, 2012) won critical acclaim and even garnered him a Pulitzer Prize, despite being panned by actual historians for its many howlers and weirdly old-fashioned historiography (see my detailed critical review here, with links to other scathing critiques by historians). Greenblatt’s account sticks closely to the nineteenth century narrative of “the dark ages” beloved by New Atheists, so it’s hardly surprising that the myths about the Great Library feature prominently in his account. Thus he informs his readers with great assurance that:
“At its height the Museum contained at least half a million papyrus rolls systematically organised, labelled and shelved according to a clever new system … alphabetical order.” (Greenblatt, p. 88)
The figure of “half a million scrolls” (or even “half a million books”) is the one that is usually bandied about, but even that colossal number is not quite enough for some polemicists. Attorney and columnist Jonathan Kirsch plumped for a much higher number in his book God Against the Gods: The History of the War Between Monotheism and Polytheism (Viking, 2004)
“In 390 AD … a mob of Christian zealots attacked the ancient library of Alexandria, a place where the works of the greatest rarity and antiquity had been collected … some 700,000 volumes and scrolls in all.” (Kirsch, p. 278)
Obviously the larger the collection in the Great Library the more terrible the tragedy of its loss, so those seeking to apportion blame for the supposed destruction of the Library usually go for these much higher numbers (it may be no surprise to learn that it’s the monotheists who are the “bad guys” in Kirsch’s cartoonish book). But did the Great Library really contain this huge number of books given that these numbers would represent a large library collection even today?
As with most things on this subject, it seems the answer is no. […] Some of these figures are interdependent, so for example Ammianus is probably depending, directly or indirectly, on Aulus Gellius for his “700,000” figure, which in turn is where Kirsch gets the same number in the quote above. Others look suspiciously precise, such as Epiphanius’ “54,800”. In summary of a lot of discussion by critical scholars, the best thing to say is that none of these figures is reliable. In her survey of the historiography of the issue, Diana Delia notes “lacking modern inventory systems, ancient librarians, even if they cared to, scarcely had the time or means to count their collections” (see Delia, “From Romance to Rhetoric: The Alexandrian Library in Classical and Islamic Traditions”, The American Historical Review, Vol. 97, No. 5, Dec. 1992, pp. 1449-67, p. 1459). Or as another historian once put it wryly “There are no statistics in ancient sources, just rhetorical flourishes made with numbers.”
One way that historians can make estimates of the size of ancient libraries is by examining the floor plans of their ruins and calculating the space their book niches would have taken up around the walls and then the number of scrolls each niche could hold. This works for some other ancient libraries for which we have surveyable remains, but unfortunately that is not the case for the Mouseion, given that archaeologists still have to guess where exactly it stood. So Columbia University’s Roger S. Bagnall has taken another tack. In a 2002 paper that debunks several of the myths about the Great Library (see Bagnall, “Alexandria: Library of Dreams”, Proceedings of the American Philosophical Society, Vol. 146, No. 4, Dec. 2002, pp. 348-362), he begins with how many authors we know were writing in the early Hellenistic period. He notes that we know of around 450 authors for whom we have, at the very least, some lines of writing whose work existed in the fourth century BC and another 175 from the third century BC. He points out that most of these writers probably only wrote works that filled a couple of scrolls at most, though a small number of them – like the playwrights – would have had a total corpus that filled many more than that, even up to 100 scrolls. So by adopting the almost certainly far too high figure of an average of 50 scrolls to contain the work of each writer, Bagnall arrives as a mere 31,250 scrolls to contain all the works of all the writers we know about to the end of the third century. He notes:
“We must then assume, to save the ancient figures for the contents of the Library, either that more than 90 percent of classical authors are not even quoted or cited in what survives, or that the Ptolemies acquired a dozen copies of everything, or some combination of these unlikely hypotheses. If we were (more plausibly) to use a lower average output per author, the hypotheses needed to save the numbers would become proportionally more outlandish.” (Bagnall, p. 353)
Bagnall makes other calculations taking into account guesses at what number of completely lost authors there may have been and still does not manage to get close to most of the figures given in our sources. His analysis makes it fairly clear that these numbers, presented so uncritically by popular authors for rhetorical effect, are probable fantasies. As mentioned above, when we can survey the archaeology of an ancient library’s ruins, some estimate can be made of its holdings. The library in the Forum of Trajan in Rome occupied a large space 27 by 20 metres and Lionel Casson estimates it could have held “in the neighbourhood of 20,000 scrolls” (Casson, p. 88). A similar survey of the remains of the Great Library of Pergamon comes to an estimate of 30,000 scrolls there. Given that this library was considered a genuine rival to the Great Library of Alexandria, it is most likely that the latter held around 40-50,000 scrolls at its height, containing a smaller number of works overall given that ancient works usually took up more than one scroll. This still seems to have made it the largest library collection in the ancient world and thus the source of its renown and later myths, but it’s a far cry from the “500,000” or “700,000” claimed by uncritical popular sources and people with axes to grind.
Tim O’Neill, “The Great Myths 5: The Destruction Of The Great Library Of Alexandria”, History for Atheists, 2017-07-02.